Khi nói tới khối lăng trụ, hẳn bạn sẽ liên tưởng tới các hình dạng khác nhau của lăng trụ. Dựa vào mặt đáy và cạnh bên mà ta có hình lăng trụ đứng, hình lăng trụ đều, …. Với hướng dẫn dưới dây bạn sẽ hiểu rõ hơn về dạng hình học này.
Trước khi biết công thức tính thể tích khối lăng trụ thì bạn cần tìm hiểu hình trụ có đặc điểm gì? Nó có những loại nào…
1. Hình lăng trụ là gì?
Một đa giác có hai mặt đáy song song và bằng nhau, mặt bên là hình bình hành thì đa giác đó gọi là hình lăng trụ.
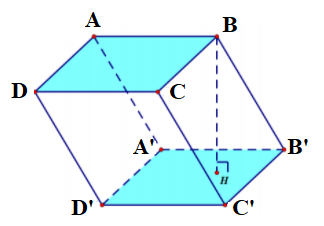
1.1 Tên gọi hình lăng trụ
Tên của hình lăng trụ người ta đặt tên theo mặt đáy. Ví dụ:
- Mặt đáy hình tam giác đều thì gọi là hình lăng trụ tam giác đều

- Mặt đáy hình tứ giác đều thì gọi là hình lăng trụ tứ giác đều

1.2 Hình lăng trụ đứng
Nếu như hình lăng trụ mà có các cạnh bên vuông góc với mặt đáy thì người ta gọi là hình lăng trụ đứng.

Lưu ý:
- Nếu mặt đáy là hình chữ nhật thì hình trụ đứng của tứ giác có tên gọi khác là hình hộp chữ nhật.
- Nếu hình trụ đứng tứ giác có 12 cạnh đều có độ dài là a thì tên gọi của nó là hình lập phương.
2. Thể tích khối lăng trụ
Công thức tính thể tích hình lăng trụ: V = B.h
Trong đó
- V là thể tích khối lăng trụ ( đơn vị m3)
- B là diện tích khối lăng trụ ( đơn vị m2)
- h là chiều cao khối lăng trụ ( đơn vị m)
3. Bài tập
Bài tập 1. Một bể nước hình trụ có diện tích mặt đáy B = 2 m2 và đường cao h = 1 m. Thể tích của bể nước này bằng bao nhiêu?
Hướng dẫn giải
Áp dụng công thức V = B.h = 2.1 = 2 m3.
Bài tập 2. Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a = 2 cm và chiều cao là h = 3 cm. Hãy tính thể tích hình lăng trụ này
Hướng dẫn giải

Vì đáy là tam giác đều cạnh a nên diện tích: ${S_{ABC}} = {a^2}.\frac{{\sqrt 3 }}{4}$ $ = {2^2}.\frac{{\sqrt 3 }}{4}$ $ = \sqrt 3 \left( {{m^2}} \right)$
Khi này, thể tích là $V = {S_{ABC}}.h = \sqrt 3 .3 = 3\sqrt 3 \left( {{m^3}} \right)$
Bài tập 3. ( Trích câu 4 đề thi tham khảo lần 2 của BGD&ĐT 2020)

Bài tập 4.

Bài tập 5.
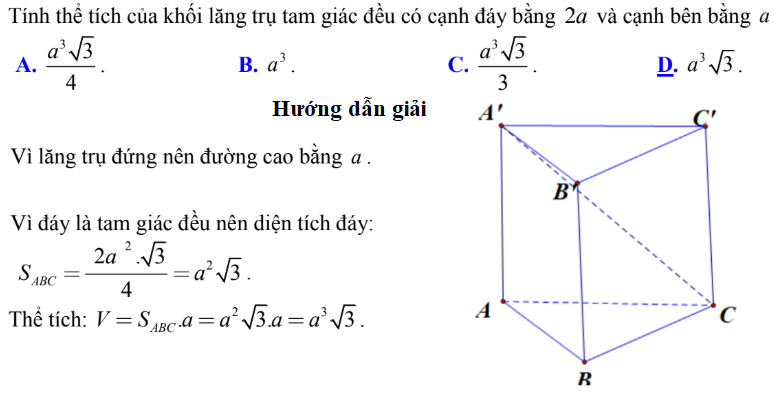
Bài tập 6.
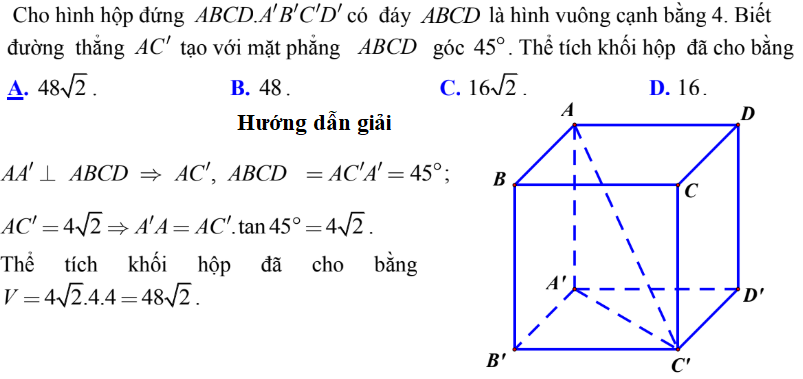
Bài tập 7.

Trên đây là các đặc điểm cũng như công thức thể tích khối hình trụ mà Toán Học đã giới thiệu với bạn. Hy vọng bài viết này hữu ích với bạn.