Khám phá cách giải chi tiết 7 câu hỏi quan trọng trong đề KSCL Toán 12 ôn thi tốt nghiệp THPT 2025 của Trường THPT Hoằng Hóa 3, Thanh Hóa. Cập nhật phương pháp giải nhanh, mẹo làm bài hiệu quả, phù hợp với định hướng ra đề mới nhất của Bộ GD&ĐT. Đừng bỏ lỡ nếu bạn muốn nâng cao điểm số và tự tin chinh phục kỳ thi THPT Quốc gia 2025!

Câu 1. Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và thỏa mãn $f\left( x \right)+2xf\left( {{x}^{2}} \right)=2{{x}^{7}}+3{{x}^{3}}-x-1$ với $x\in \mathbb{R}$. Các khẳng định sau đúng hay sai?
a) $f\left( 0 \right)=-1.$
b) $f\left( 1 \right)=2.$
c) $f\left( 2 \right)+f(-2)=-2.$
d) $\int\limits_{0}^{1}{f\left( x \right)\text{d}x}=-\frac{1}{4}.$
Lời giải
Chọn a) Đúng | b) Sai | c) Đúng | d) Đúng.
a) Từ $f\left( x \right)+2xf\left( {{x}^{2}} \right)=2{{x}^{7}}+3{{x}^{3}}-x-1\,\,\,\left( 1 \right)$
Thay $x=0$ vào $\left( 1 \right)$ ta được: $f\left( 0 \right)=-1$
Suy ra mệnh đề a) đúng.
b) Từ $f\left( x \right)+2xf\left( {{x}^{2}} \right)=2{{x}^{7}}+3{{x}^{3}}-x-1\,\,\,$
Thay $x=1$ vào $\left( 1 \right)$ ta được $f\left( 1 \right)+2f\left( 1 \right)=3\Rightarrow f\left( 1 \right)=1\,\,$
Suy ra mệnh đề b) sai.
c) Thay $x=2$ vào $\left( 1 \right)$ ta được: $f\left( 2 \right)+4f\left( 4 \right)=277$
Thay $x=-2$ vào $\left( 1 \right)$ ta được: $f\left( -2 \right)-4f\left( 4 \right)=-279$
Do đó: $f\left( 2 \right)+f\left( -2 \right)=277-279=-2$
Suy ra mệnh đề c) đúng.
d) Từ $\left( 1 \right)$ta có $\int\limits_{0}^{1}{f\left( x \right)\text{d}}x+\int\limits_{0}^{1}{2xf\left( {{x}^{2}} \right)\text{d}}x=\int\limits_{0}^{1}{\left( 2{{x}^{7}}+3{{x}^{3}}-x-1 \right)\,\text{d}}x$
$\Rightarrow \int\limits_{0}^{1}{f\left( x \right)\text{d}}x+\int\limits_{0}^{1}{f\left( {{x}^{2}} \right).{{\left( {{x}^{2}} \right)}^{\prime }}\text{d}}x=-\frac{1}{2}$
Gọi $F(x)$ nguyên hàm của $f\left( x \right)$.
Khi đó $\int\limits_{0}^{1}{f\left( {{x}^{2}} \right).{{\left( {{x}^{2}} \right)}^{\prime }}\text{d}}x=\,\,F\left( {{x}^{2}} \right)\left| \begin{align} & 1 \\ & 0 \\ \end{align} \right.=F(1)-F(0)=\int\limits_{0}^{1}{f\left( x \right)\text{d}}x$
Do đó $\int\limits_0^1 {f\left( x \right){\rm{d}}} x + \int\limits_0^1 {f\left( {{x^2}} \right).{{\left( {{x^2}} \right)}^\prime }{\rm{d}}} x = – \frac{1}{2}$ $ \Rightarrow 2\int\limits_0^1 {f\left( x \right){\rm{d}}} x = – \frac{1}{2}$ $ \Rightarrow \int\limits_0^1 {f\left( x \right){\rm{d}}} x = – \frac{1}{4}\,\,$
Suy ra mệnh đề d) đúng.
Câu 2. Trong không gian $Oxyz$, cho ba điểm $A\left( 0;0;-1 \right),\,\,B\left( -1;1;0 \right),\,\,C\left( 1;0;1 \right)$. Các khẳng định sau đúng hay sai
a) Điểm $I(\frac{-1}{2};\frac{1}{2};\frac{-1}{2})$ là trung điểm của đoạn thẳng $AB$.
b) Khi tứ giác $ABC\text{D}$ là hình bình hành thì $O\text{D}=\sqrt{6}$.
c) Điểm $H(\frac{1}{3};\frac{5}{3};\frac{-1}{3})$ là chân đường cao kẻ từ $A$xuống cạnh $BC$ của tam giác $ABC$.
d) Biết điểm $M(x;y;z)$ để biểu thức $3M{{A}^{2}}+2M{{B}^{2}}-M{{C}^{2}}$ đạt giá trị nhỏ nhất, khi đó $4x\,\text{-}\,\text{2y}\,\text{+}\,\text{z}\ =-5$.
Lời giải
Chọn a) Đúng | b) Sai | c) Sai | d) Đúng.
a) Toạ độ trung điểm $I$ của đoạn thẳng $AB$ là $I\left( \frac{0-1}{2};\frac{0+1}{2};\frac{-1+0}{2} \right)\text{ hay I}\left( \frac{-1}{2};\frac{1}{2};\frac{-1}{2} \right).$
Vậy a) đúng.
b) Gọi $D\left( x;\,y;\,z \right)$. Để tứ giác $ABCD$ là hình bình hành thì
$\overrightarrow {AB} = \overrightarrow {DC} $ $ \Rightarrow \left\{ \begin{array}{l} – 1 = 1 – x\\ 1 = 0 – y\\ 1 = 1 – z \end{array} \right.$ $ \Rightarrow D\left( {2;{\mkern 1mu} – 1;{\mkern 1mu} 0} \right) \Rightarrow O{\rm{D}} = \sqrt 5 .$
Vậy b) sai.
c) Ta có $\overrightarrow{BC}=(2;-1;1)$.
Gọi $H(x;y;z)$ là chân đường cao kẻ từ $A$xuống cạnh $BC$ của tam giác $ABC$.
Suy ra $\overrightarrow{BH}=(x+1;y-1;z)$.
Ta có $\left\{ \begin{array}{l} \overrightarrow {BH} //\overrightarrow {BC} \\ \overrightarrow {AH} \bot \overrightarrow {BC} \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x + 1 = 2t;y – 1 = – t;z = t\,\,\left( 1 \right)\\ \overrightarrow {AH} \cdot \overrightarrow {BC} = 0\,\,\,\,\left( 2 \right) \end{array} \right.$
$\left( 1 \right)\Rightarrow H(2t-1;-t+1;t)$$\Rightarrow \overrightarrow{AH}=(2t-1;-t+1;t+1)$.
$\left( 2 \right)\Rightarrow 2.(2t-1)-(-t+1)+t+1=0$$\Leftrightarrow 6t=2\Leftrightarrow t=\frac{1}{3}\Rightarrow $ $H(\frac{-1}{3};\frac{2}{3};\frac{1}{3})$.
Vậy c) sai.
d)
$M\left( {x;y;z} \right) \Rightarrow \left\{ \begin{array}{l} \overrightarrow {AM} = \left( {x;y;z + 1} \right)\\ \overrightarrow {BM} = \left( {x + 1;y – 1;z} \right)\\ \overrightarrow {CM} = \left( {x – 1;y;z – 1} \right) \end{array} \right.$ $ \Rightarrow \left\{ \begin{array}{l} A{M^2} = {x^2} + {y^2} + {\left( {z + 1} \right)^2}\\ B{M^2} = {\left( {x + 1} \right)^2} + {\left( {y – 1} \right)^2} + {z^2}\\ C{M^2} = {\left( {x – 1} \right)^2} + {y^2} + {\left( {z – 1} \right)^2} \end{array} \right.$ $ \Rightarrow P = 3M{A^2} + 2M{B^2} – M{C^2}$
$=3\left[ {{x}^{2}}+{{y}^{2}}+{{\left( z+1 \right)}^{2}} \right]+2\left[ {{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{z}^{2}} \right]-\left[ {{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-1 \right)}^{2}} \right]$
$ = 4{x^2} + 4{y^2} + 4{z^2} + 6x – 4y + 8z + 5$ $ = {\left( {2x + \frac{3}{2}} \right)^2} + {\left( {2y – 1} \right)^2} + {\left( {2z + 2} \right)^2} – \frac{9}{4} \ge – \frac{9}{4}$.
$\Rightarrow MinP=-\frac{9}{4}$ $\Leftrightarrow x=-\frac{3}{4}$, $y=\frac{1}{2}$, $z=-1$, khi đó $M\left( -\frac{3}{4};\frac{1}{2};-1 \right)$.
Vậy $P=4x\,\text{-}\,\text{2y}\,\text{+}\,\text{z}\ \text{=}\,\text{-3}\,\text{-}\,\text{1}\,\text{-}\,\text{1}\,\text{=}\,\text{-}\,\text{5}\text{.}$
Vậy d) đúng.
Câu 3.Trong không gian với hệ tọa độ $Oxyz$ cho đường thẳng $\Delta :\frac{x}{-1}=\frac{y+3}{2}=\frac{z-2}{3}$ và mặt phẳng $\left( P \right):x+2y-z+2025=0$. Các khẳng định sau đúng hay sai?
a) Đường thẳng $\Delta $ có vectơ chỉ phương là $\overrightarrow{u}=\left( 1;-2;-3 \right)$
b) Góc giữa đường thẳng $\Delta $ và mặt phẳng $\left( P \right)$ bằng $90{}^\circ $.
c) Đường thẳng ${{d}_{1}}$ là giao tuyến của $\left( P \right)$ và mặt phẳng $\left( Oxy \right)$ Gọi $\alpha $ là góc giữa ${{d}_{1}}$ và mặt phẳng $\left( Oxz \right)$. Khi đó $\alpha >30{}^\circ $.
d) Đường thẳng ${{d}_{2}}$ vuông góc với $\left( P \right)$ và tạo với $\left( Q \right):x+my-3=0$ một góc $30{}^\circ $. Khi đó tổng các giá trị của tham số $m$ bằng $\frac{8}{5}$.
Lời giải
Chọn a) Đúng | b) Sai | c) Sai | d) Sai
a) Đường thẳng Δ có vectơ chỉ phương là \(\vec{u} = (-1;2;3) = – (1;-2;-3)\)
b) Góc giữa đường thẳng Δ và mặt phẳng (P) bằng \(0^\circ\). (P) có VTPT \(\vec{n} = (1;2;-1)\)
Do đó $ \sin(\angle(\Delta, (P))) = \left|\cos(\vec{u}, \vec{n})\right| = \left|\frac{\vec{u} \cdot \vec{n}}{|\vec{u}||\vec{n}|}\right| = \left|\frac{-1 \cdot 1 + 2 \cdot 2 + 3 \cdot (-1)}{\sqrt{14} \cdot \sqrt{6}}\right| = 0 $
Vậy \(\angle(\Delta, (P)) = 0^\circ\)
c) Đường thẳng \(d_1\) là giao tuyến của \((P)\) và mặt phẳng \((Oxy)\). Gọi \(\alpha\) là góc giữa \(d_1\) và mặt phẳng \((Oxz)\). Khi đó \(\alpha > 30^\circ\).
$ (Oxy) \text{ có VTPT là } \vec{k} = (0;0;1), \quad (Oxz) \text{ có VTPT là } \vec{j} = (0;1;0), \quad (P) \text{ có VTPT là } \vec{n} = (1;2;-1) $ $ d = (P) \cap (Oxy) \Rightarrow d \text{ có VTCP là } \vec{u}_d = \left[ \vec{k}, \vec{n} \right] = (-2;1;0) $ $ \sin \beta = \left| \cos(\vec{u}_d, \vec{j}) \right| = \left| \frac{1}{\sqrt{5}} \right| \Rightarrow \beta \approx 27^\circ < 30^\circ $
d) Đường thẳng \(d_2\) vuông góc với \((P)\) và tạo với \((Q): x + my – 3 = 0\) một góc \(30^\circ\). Khi đó tổng các giá trị của tham số \(m\) bằng \(\dfrac{-8}{5}\).
Đường thẳng \(d_2\) vuông góc với \((P)\) nên có VTCP là \(\vec{u}_{d_2} = (1;2;-1)\).
\((Q)\) VTPT là \(\vec{n}_{(Q)} = (1;m;0)\).
$ \sin(d_2, (Q)) = \left| \cos(\vec{n}_Q, \vec{u}_{d_2}) \right| = \left| \frac{1 + 2m}{\sqrt{6} \cdot \sqrt{m^2 + 1}} \right| = \frac{1}{2} $ $ \Leftrightarrow 2|1 + 2m| = \sqrt{6} \cdot \sqrt{m^2 + 1} $ $ \Leftrightarrow 2(1 + 4m + 4m^2) = 3(m^2 + 1) $ $ \Leftrightarrow 5m^2 + 8m – 1 = 0 \Leftrightarrow m = \frac{-4 \pm \sqrt{21}}{5} $
Vậy tổng các giá trị của tham số \(m\) bằng \(\dfrac{-8}{5}\).
Câu 4. Một hồ nước nhân tạo được xây dựng trong công viên giải trí. Trong mô hình minh họa sau, nó được giới hạn bởi các trục tọa độ và đồ thị hàm số $y=f\left( x \right)=\frac{1}{10}\left( -{{x}^{3}}+9{{x}^{2}}-15x+56 \right)$
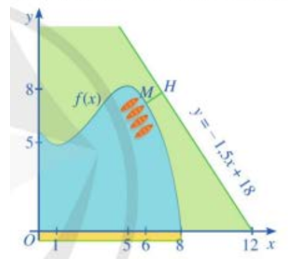
Đơn vị đo độ dài trên mỗi trục tọa độ là 100m. Trong công viên có một con đường chạy dọc theo đồ thị của hàm số $y=-\frac{3}{2}x+18$. Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước sao cho khoảng cách từ bến thuyền đến con đường là ngắn nhất . Khi đó tọa độ của điểm để xây bến thuyền là $M\left( a;b \right)$. Tính $T=a-b$.
Lời giải
Đáp án: -1,4
Do $f(x)$ là hàm số liên tục trên $\mathbb{R}$nên điểm M gần đường thẳng $d:y=-\frac{3}{2}x+18$ nhất thì tiếp tuyến của hàm số $y=f\left( x \right)$ tại M song song với d
$ \Rightarrow f’\left( x \right) = – \frac{3}{2}$ $ \Leftrightarrow \frac{1}{{10}}\left( { – 3{x^2} + 18x – 15} \right) = – \frac{3}{2}$ $ \Leftrightarrow – {x^2} + 6x = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 6 \end{array} \right.$
Khi đó $M\left( 0;\frac{28}{5} \right)$ và $M\left( 6;\frac{37}{5} \right)$
Dựa trên đồ thị ta thấy $M\left( 6;\frac{37}{5} \right)$ là điểm trên đồ thị hàm số $y=f\left( x \right)$ có khoảng cách đến đường thẳng d là nhỏ nhất.
Do đó $a=6,b=\frac{37}{5}\Rightarrow a-b=-1,4$.
Câu 5.Một nhà máy nhiệt điện sử dụng 90 máng Parabol thu nhiệt năng lượng mặt trời có cùng kích thước, bề mặt cong đều nhau (tham khảo hình vẽ). Mỗi máng có chiều rộng $2m$, bề dày của khối silic làm mặt máng là $2dm$, chiều dài $3m$. Đặt máng tiếp giáp mặt đất có điểm cao nhất của khối silic làm mặt máng so với mặt đất là $5dm$. Khi đó thể tích (tính theo đơn vị ${{m}^{3}}$) của khối silic làm $90$ mặt máng bằng bao nhiêu ?

Lời giải
Đáp án: 108
Gọi đường cong tương ứng với vành trên và vành dưới của máng lần lượt là $\left( {{P}_{1}} \right)$ và $\left( {{P}_{2}} \right)$.
Xét hệ trục tọa độ $Oxy$ như hình vẽ
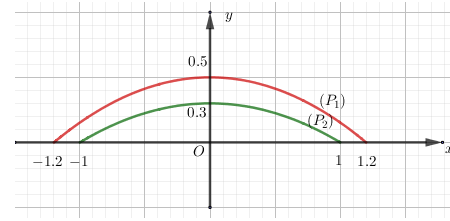
Khi đó Parabol $\left( {{P}_{1}} \right)$ và $\left( {{P}_{2}} \right)$đều có dạng $y=a{{x}^{2}}+b$.
$\left( {{P}_{1}} \right)$ đi qua các điểm có tọa độ $\left( -1,2;0 \right)$;$\left( 1,2;0 \right)$; $\left( 0;0,5 \right)$.
$\left( {{P}_{2}} \right)$ đi qua các điểm có tọa độ $\left( -1;0 \right)$;$\left( 1;0 \right)$; $\left( 0;0,3 \right)$.
Suy ra $\left( {{P}_{1}} \right):y=-\frac{25}{72}{{x}^{2}}+\frac{1}{2}$ và $\left( {{P}_{2}} \right):y=-\frac{3}{10}{{x}^{2}}+\frac{3}{10}$.
Diện tích mặt cắt của máng Parabol là
$S=2\left[ \int\limits_{0}^{1,2}{\left( -\frac{25}{72}{{x}^{2}}+\frac{1}{2} \right)dx-\int\limits_{0}^{1}{\left( -\frac{3}{10}{{x}^{2}}+\frac{3}{10} \right)dx}} \right]=\frac{2}{5}\left( {{m}^{2}} \right)$.
Vậy thể tích của khối silic làm $90$ mặt máng là $V=90.\frac{2}{5}.3=108\left( {{m}^{3}} \right)$.
Câu 6. Trong không gian hệ trục tọa độ Oxyz (đơn vị trên mỗi trục là kilômét), đài kiểm soát không lưu sân bay Cam Ranh – Khánh Hòa ở vị trí $O\left( 0;0;0 \right)$ và được thiết kế phát hiện máy bay ở khoảng cách tối đa $600\,\text{km}$. Một máy bay của hãng Việt Nam Airlines đang ở vị trí $M\left( -1000;-200;10 \right)$ chuyển động với vận tốc không đổi $900\,\text{km/h}$, chuyển động theo đường thẳng $d$ có vectơ chỉ phương là $\overrightarrow{u}=\left( 100;80;0 \right)$ và hướng về đài kiểm soát không lưu (như hình vẽ).
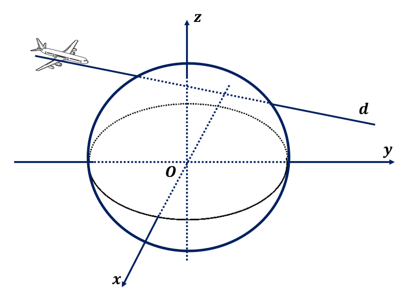
Hỏi trên đường bay của mình, thời gian nhiêu phút thì máy bay, bay qua vùng kiểm soát không lưu? (kết quả làm tròn đến hàng đơn vị)
Lời giải
Đáp án: 50
Ranh giới vùng phủ sóng của đài kiểm soát không lưu là mặt cầu $\left( S \right)$ tâm $O\left( 0;0;0 \right)$ bán kính $R=600\,\text{km}$.
Phương trình mặt cầu $\left( S \right)$ là: ${{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{600}^{2}}$.
Thay phương trình $\left( d \right):\left\{ \begin{align} & x=-1000+100t \\ & y=-200+80t \\ & z=10 \\ \end{align} \right.\left( t\in \mathbb{R} \right)$ vào $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{600}^{2}}$.
Ta được: ${{\left( 100t-1000 \right)}^{2}}+{{\left( 80t-200 \right)}^{2}}+{{10}^{2}}={{600}^{2}}$
$ \Leftrightarrow 16400{t^2} – 232000t + 680100 = 0$ $ \Leftrightarrow \left[ \begin{array}{l} t \approx 10 \Rightarrow B\left( {0;600;10} \right)\\ t \approx 4,15 \Rightarrow C\left( { – 585;132;10} \right) \end{array} \right.$
Khi đó, quãng đường mà máy bay di chuyển qua vùng kiểm soát không lưu là
$S=BC=\sqrt{{{\left( -585 \right)}^{2}}+{{\left( 132-600 \right)}^{2}}}\approx 749$
Thời gian máy bay, bay qua vùng kiểm soát không lưu là: $t=\frac{749}{900}\approx 0,83\left( \text{h} \right)\approx 50$ (phút)
Câu 7. Nhà nghiên cứu chọn một nhóm người đàn ông, với mỗi người trong nhóm, nhà nghiên cứu kiểm tra xem họ có nghiện thuốc lá và bị viêm phổi hay không. Kết quả được thống kê trong bảng sau:
| viêm phổi | Không viêm phổi | |
| Nghiện thuốc lá | 750 | 1238 |
| Không nghiện thuốc lá | 472 | y |
Hỏi nhà nghiên cứu phải tiến hành kiểm tra tối thiểu bao nhiêu người đàn ông thì xác suất để người đó bị viêm phổi trong khi người đó không nghiện thuốc lá không vượt quá $\frac{1}{7}$.
Lời giải
Đáp án: 5292
Gọi $A$ là biến cố: “Người đó bị viêm phổi”
Gọi $B$ là biến cố: “Người đó không nghiện thuốc lá” $\Rightarrow n\left( B \right)=472+y$
Khi đó $AB$ là biến cố: “Người đó bị viêm phổi và không nghiện thuốc lá”. Vậy $n(AB)=472$.
xác suất để người đó bị viêm phổi trong khi người đó không nghiện thuốc lá là
$P\left( A\backslash B \right)=\frac{P\left( AB \right)}{P\left( B \right)}=\frac{n\left( AB \right)}{n\left( B \right)}=\frac{472}{472+y}\le \frac{1}{7}\Leftrightarrow y\ge 2832$. Vậy nhà nghiên cứu phải tiến hành kiểm tra tối thiểu $750+1238+472+2832=5292$người đàn ông thì xác suất để người đó bị viêm phổi trong khi người đó không nghiện thuốc lá không vượt quá $\frac{1}{7}$.